Have you ever wondered about the intricate beauty of shapes? From the sharp edges of a snowflake to the smooth curves of a circle, geometry holds a hidden world of fascination. Among these geometric marvels are regular polygons, captivating with their symmetric elegance and predictable properties. Today, we delve into the intriguing world of 10 3 areas of regular polygons, uncovering their unique characteristics and exploring their applications in various fields.

Image: www.youtube.com
Understanding the areas of regular polygons is a fundamental concept in geometry, revealing the relationships between sides, angles, and the space they enclose. Whether you’re studying for an exam, engaging in a playful puzzle, or seeking an appreciation for the elegance of mathematical patterns, these fascinating shapes have something to offer.
The Basics of Regular Polygons
Before diving into the 10 3 areas of regular polygons, let’s define our key players. A polygon is a closed shape formed by straight line segments. A regular polygon takes this definition a step further, requiring all sides to be of equal length and all angles to be equal in measure. Think of a square, where all sides are the same and all corners form right angles, or a hexagon, with six equal sides and angles. This inherent symmetry gives regular polygons their alluring charm.
The Power of Formulae: Calculating Areas
The area of a polygon, in essence, is the amount of space it occupies. For regular polygons, we have a special tool in our arsenal – a simple formula to calculate their area:
Area = (1/2) × Perimeter × Apothem
Let’s break down the components:
- Perimeter: The sum of all side lengths of the regular polygon.
- Apothem: The perpendicular distance from the center of the polygon to the midpoint of any side. Think of it as the “radius” of the regular polygon!
This formula unveils a beautiful connection between the sides and angles of a regular polygon and its enclosed space. It allows us to calculate the area of any regular polygon, from a simple triangle to a complex dodecagon, with just a few measurements.
The 10 3 Areas of Regular Polygons: Unveiling the Mysteries
Now, let’s explore the intriguing concept of 10 3 areas of regular polygons. This refers to the areas enclosed by various regular polygons with a side length of 3 units.
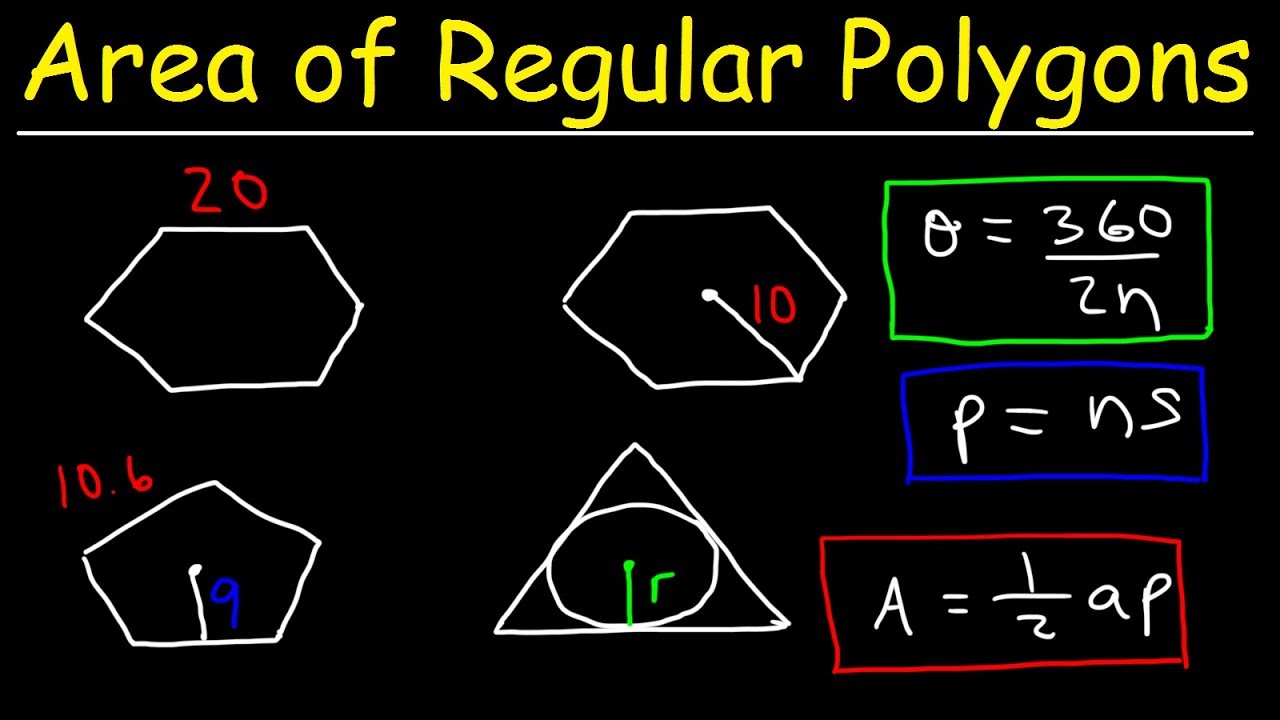
Image: printablelistelena.z22.web.core.windows.net
1. Triangle: Area = 3.897
The triangle, with its three equal sides, marks the beginning of our journey. Its area, calculated using the formula, is approximately 3.897 square units.
2. Square: Area = 9
The square, with its four equal sides and right angles, boasts an area of 9 square units. Its straightforward shape makes it an easy one to calculate!
3. Pentagon: Area = 13.75
The pentagon, with its five equal sides, is where things get interesting. Its area, despite its intricate shape, is calculated to be approximately 13.75 square units.
4. Hexagon: Area = 23.383
The hexagon, with its six equal sides, exhibits a more complex shape. Its area, calculated using the formula, is approximately 23.383 square units.
5. Heptagon: Area = 33.71
The heptagon, with its seven equal sides, is a seven-sided shape with an area of approximately 33.71 square units.
6. Octagon: Area = 45.254
The octagon, with its eight equal sides, is a captivating shape with an area of approximately 45.254 square units.
7. Nonagon: Area = 58.006
The nonagon, the nine-sided shape, holds a unique beauty with its area calculated to be approximately 58.006 square units.
8. Decagon: Area = 72.008
The decagon, with its ten equal sides, is a fascinating shape with an area of approximately 72.008 square units.
9. Hendecagon: Area = 87.29
The hendecagon, an eleven-sided shape, is more complex, but still captivating with its area of 87.29 square units.
10. Dodecagon: Area = 103.82
The dodecagon, with its twelve equal sides, is a majestic shape with an area of approximately 103.82 square units.
Real-World Applications of Regular Polygons
Regular polygons aren’t just theoretical shapes confined to geometry textbooks. They have found practical applications in a multitude of fields:
- Architecture: Regular polygons are frequently used in architecture, from simple designs like square windows to intricate tessellations in floor tiles.
- Engineering: Engineers use regular polygons for a variety of structures. For example, the hexagonal honeycomb structure is incredibly strong and lightweight, often used in aircraft and construction.
- Art and Design: Regular polygons are ubiquitous in art and design. They are often used for patterns and ornaments, reflecting their inherent symmetry and pleasing proportions.
- Nature: From the hexagonal cells of a honeycomb to the pentagonal symmetry of a starfish, nature exhibits regular polygons in fascinating ways.
10 3 Areas Of Regular Polygons
Exploring Further: A World of Regular Polygons
The 10 3 areas of regular polygons offer only a glimpse into the fascinating world of these geometric shapes. Further exploration can lead to a deeper understanding of the relationships between sides, angles, areas, and the beauty of these symmetrical shapes. Dive into the world of geometry, uncover the wonders of regular polygons, and be amazed by the mathematical elegance that surrounds us!





