Remember that time you were trying to figure out if there was a connection between watching too much TV and having trouble sleeping? Maybe you decided to survey your friends and family and record their answers. But then a big question came up: how do you analyze all this data to see if there’s a real pattern? That’s where the chi-square test of independence comes in!
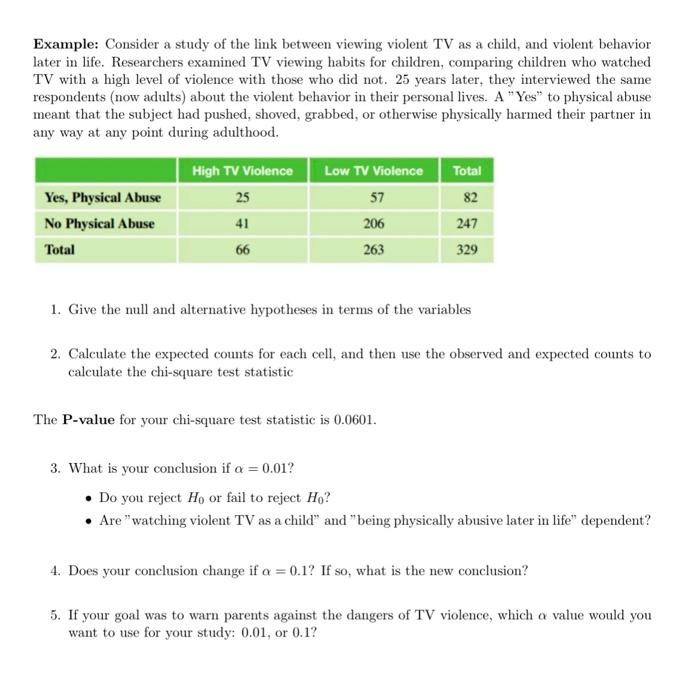
Image: www.chegg.com
The chi-square test of independence is a powerful statistical tool that lets you examine the relationship between two categorical variables. It helps you determine if there’s a significant association or if the observed differences are just due to chance. In this article, we’ll explore how to use the chi-square test of independence, walk through some example problems with detailed solutions, and even provide you with resources for practice PDFs.
Understanding the Chi-Square Test of Independence
The chi-square test of independence is used to assess whether there is a statistically significant relationship between two categorical variables. Unlike other statistical tests, it doesn’t compare means or averages; instead, it analyzes the distribution of frequencies within each category.
Imagine you have two groups of people, let’s say those who prefer to watch movies at home and those who prefer to go to the cinema. You want to know if there is a connection between their preferred movie-watching choice and their age group (young adults versus older adults). This is where the chi-square test comes in handy.
How the Chi-Square Test Works
The test works by comparing the observed frequencies (actual counts within each category) to the expected frequencies (counts you would expect if the two variables were independent). If there is a significant difference between the observed and expected frequencies, it suggests that these variables are not independent but rather related to each other. This relationship could be positive, negative, or simply demonstrate a dependence.
Here’s how you would conduct the chi-square test:
- Set up your hypothesis: You need null and alternative hypotheses. The null hypothesis states that there is no association between your two variables. The alternative hypothesis states that a relationship exists. For example:
- Null hypothesis: There is no association between preferred movie-watching choice and age group.
- Alternative hypothesis: There is an association between preferred movie-watching choice and age group.
- Establish your significance level: This is usually set at 0.05 which means there is a 5% chance of finding a relationship when there isn’t one. This is a standard in scientific studies.
- Create a contingency table: Organize your data into a table with rows representing one variable (e.g., age groups) and columns representing the other (e.g., preferred movie-watching choice).
- Calculate the expected frequencies: Use the marginal totals from your contingency table to calculate the expected frequencies for each cell if the two variables were independent.
- Calculate the chi-square statistic: This is measured based on the difference between the observed frequencies and the expected frequencies.
- Determine the degrees of freedom: This is the number of independent pieces of information that contribute to the value of the chi-square statistic. For a contingency table with ‘r’ rows and ‘c’ columns, degrees of freedom are calculated as (r-1) * (c-1).
- Look up the critical value: Based on your significance level and degrees of freedom use a chi-square distribution table to determine the critical value.
- Compare the calculated chi-square statistic to the critical value: This will be used to determine if the result is statistically significant.
We will see how this applies in the example problems.
Example Problems with Answers

Image: www.pdfprof.com
Example Problem 1: Movie Preferences and Age
Let’s go back to our movie preferences example. Say you surveyed 100 people and obtained the following data:
| Home | Cinema | Total | |
|---|---|---|---|
| Young Adults | 40 | 10 | 50 |
| Older Adults | 20 | 30 | 50 |
| Total | 60 | 40 | 100 |
Question: Is there a statistically significant association between age group and preferred movie-watching choice at a 0.05 significance level?
Solution:
- Hypotheses:
- Null hypothesis (H0): There is no association between age group and preferred movie-watching choice.
- Alternative hypothesis (H1): There is an association between age group and preferred movie-watching choice.
- Significance level (α): α = 0.05.
- Expected frequencies:
- Calculate the chi-square statistic:
- Degrees of freedom: (r – 1) * (c – 1) = (2 – 1) * (2 – 1) = 1
- Critical value: Using a chi-square distribution table, the critical value for a significance level of 0.05 and 1 degree of freedom is 3.841.
- Comparison: Since the calculated chi-square statistic (16.67) is greater than the critical value (3.841), we reject the null hypothesis.
| Home | Cinema | Total | |
|---|---|---|---|
| Young Adults | 30 (50 * 60/100) | 20 (50 * 40/100) | 50 |
| Older Adults | 30 (50 * 60/100) | 20 (50 * 40/100) | 50 |
| Total | 60 | 40 | 100 |
χ2 = Σ [(Oi – Ei)2 / Ei]
χ2 = [(40 – 30)2 / 30] + [(10 – 20)2 / 20] + [(20 – 30)2 / 30] + [(30 – 20)2 / 20]
χ2 = 10/3 + 5 + 10/3 + 5
χ2 = 20/3 + 10
χ2 = 16.67
Conclusion: There is statistically significant evidence to suggest an association between age group and preferred movie-watching choice. Young adults tend to prefer watching movies at home, while older adults tend to prefer going to the cinema.
Example Problem 2: Coffee Consumption and Mood
You want to investigate whether there is a connection between a person’s daily coffee consumption and their general mood. You survey 200 people with the following results:
| Low Coffee | Moderate Coffee | High Coffee | Total | |
|---|---|---|---|---|
| Positive Mood | 30 | 45 | 25 | 100 |
| Neutral Mood | 20 | 35 | 15 | 70 |
| Negative Mood | 10 | 15 | 10 | 35 |
| Total | 60 | 95 | 50 | 200 |
Question: Is there a statistically significant association between coffee consumption and mood using a 0.01 significance level?
Solution:
- Hypotheses:
- Null hypothesis (H0): There is no association between coffee consumption and mood.
- Alternative hypothesis (H1): There is an association between coffee consumption and mood.
- Significance level (α): α = 0.01.
- Expected frequencies:
- Calculate the chi-square statistic:
- Degrees of freedom: (r – 1) * (c – 1) = (3 – 1) * (3 – 1) = 4
- Critical value: Looking at the chi-square distribution table with 4 degrees of freedom and a significance level of 0.01, the critical value is 13.277.
- Comparison: The calculated chi-square statistic (1.837) is less than the critical value (13.277). We fail to reject the null hypothesis.
| Low Coffee | Moderate Coffee | High Coffee | Total | |
|---|---|---|---|---|
| Positive Mood | 30 (100 * 60/200) | 47.5 (100 * 95/200) | 25 (100 * 50/200) | 100 |
| Neutral Mood | 21 (70 * 60/200) | 33.25 (70 * 95/200) | 17.5 (70 * 50/200) | 70 |
| Negative Mood | 9 (35 * 60/200) | 14.25 (35 * 95/200) | 7.5 (35 * 50/200) | 35 |
| Total | 60 | 95 | 50 | 200 |
χ2 = Σ [(Oi – Ei)2 / Ei]
χ2 = [(30 – 30)2 / 30] + [(45 – 47.5)2 / 47.5] + [(25 – 25)2 / 25] + [(20 – 21)2 / 21] + [(35 – 33.25)2 / 33.25] + [(15 – 17.5)2 / 17.5] + [(10 – 9)2 / 9] + [(15 – 14.25)2 / 14.25] + [(10 – 7.5)2 / 7.5]
χ2 = 0.126 + 0.126 + 0.114 + 0.048 + 0.091 + 0.357 + 0.111 + 0.031 + 0.833
χ2 = 1.837
Conclusion: There is no statistically significant evidence to suggest an association between coffee consumption and mood at the 0.01 significance level. This means that the difference in mood observed between different coffee consumption categories is likely due to chance. The null hypothesis is not rejected, so the relationship seems to be a bit more tenuous.
Tips and Expert Advice
To make the most of the chi-square test of independence, follow these expert-backed tips:
- Ensure independent observations: Your data points must be independent of each other. This means that the response of one subject should not influence the response of another.
- Use sufficiently large sample sizes: The chi-square test works best when each cell of your contingency table has at least five observed frequencies. Too few observations could lead to misleading results.
- Beware of small expected frequencies: Having small expected frequencies (e.g., less than 5) might result in misleading results. You may need to consider combining categories or using a different statistical test like Fisher’s exact test.
- Visualize your data: A well-formatted contingency table and possibly a bar chart can help you quickly understand the relationship between your variables.
By adhering to these best practices, you’ll increase the accuracy and reliability of your chi-square analysis.
FAQ
Q: What are some common applications of the chi-square test of independence?
It is frequently used in a variety of fields, including:
- Medical research: To investigate the association between smoking and lung cancer, or between gender and the effectiveness of a specific treatment.
- Marketing research: To analyze the relationship between advertising campaigns and customer purchases.
- Social science research: To study the relationship between education level and income, or between race and the likelihood of being arrested.
- Educational research: To explore the association between teaching methods and student achievement.
- Environmental research: To assess the connection between pollution levels and health outcomes.
Q: What are the limitations of the chi-square test of independence?
The chi-square test of independence has a few significant limitations to consider:
- It only works for categorical variables: It cannot be used to analyze relationships between continuous variables (like height or weight).
- It can be sensitive to sample size: Small samples can produce inaccurate results. Ensure your data is sufficiently large for reliable analysis.
- It doesn’t tell you the strength of the relationship: While it can suggest an association, it doesn’t reveal how strong or weak that relationship is.
- It can be affected by expected frequencies: Small expected frequencies can cause misleading results. Make sure your data is properly organized.
Q: Where can I find practice problems and PDFs?
Many online resources offer practice problems and even downloadable PDFs to help you master the chi-square test of independence. Consider searching for “chi-square test of independence practice problems PDF” or “chi-square test of independence examples with answers PDF” using your preferred search engine.
Additionally, textbooks on statistics and statistical software documentation for programs like SPSS or R often include detailed examples and exercises with walkthroughs, making it easier to learn and practice using the chi-square test.
Chi-Square Test Of Independence Example Problems With Answers Pdf
Conclusion
The chi-square test of independence is an invaluable tool for researchers and analysts looking to investigate the relationship between categorical variables. By following the steps outlined in this guide and using the tips provided, you can confidently apply this statistical test to analyze your data and draw meaningful conclusions. Are you ready to explore more about the chi-square test of independence? Share your thoughts in the comments section below!





